The Great  Vedic Mathematics 

I'm new to Vedic Mathematics. I searched web to get more information about the Vedic mathematics. Here I'm displaying some of  the information which I got from different web sites. I' m just intended to give some information regarding this great thing.

The term vedic mathematics refers to the group of sixteen sutras (word formulae) given by Swami Bharathi Krishna Tirthaji and the application of them to solve problems in different branches of mathematics like arithmetic, algebra etc.  He found that all problems in pure and applied mathematics can be solved easily with the aid of sixteen sutras,  or word-formulae: for example By One More than the One Before, or Vertically and Crosswise. It offers a new approach to mathematics and mathematics education.  The sutras give a set of natural principles that help to quickly solve all sorts of mathematical problems in pure and applied mathematics. 

The vedic methods are direct, beautifully interrelated, flexible, much more unified and flowing than traditional mathematics.  The methods are truly extraordinary in efficiency and simplicity.  Compexly arranged modern mathematical problems can easily be done by simple mental mathematics through these methods. 

It is peculiar to arithmetic that once the basic facts are understood any intelligent person can construct the whole science: the science of numbers develops in a totally natural way. Vedic Mathematics uses this very fact. It is based purely on sixteen Sutras, or aphorisms (word formulae). These describe the way the mind naturally works and are therefore a great help in directing the student to the appropriate method of solution. Some examples of sutras are Ekadhikena Purvena Sutra (By one more than the one before) and Urdhwa-tiryagbhyam Sutra (Vertically Crosswise). These are illustrated below.

The most striking feature of the Vedic system is its coherence. Instead of a hotch-potch of unrelated techniques the whole system is beautifully interrelated and unifed, making it extremely easy to understand. This quality makes mathematics easy and enjoyable and encourages innovation. Students can invent their own methods, they are not limited to the one 'correct' method. This leads to more creative, interested and intelligent thinking. Thus, 'difficult' problems or huge sums can often be solved immediately by the Vedic method.

VEDIC MATHEMATICS SUTRAS*

SUTRAS

SUB-SUTRAS OR COROLLARIES
By One More than the One Before                       Proportionately
All from 9 and the Last from 10 The Remainder Remains Constant
Vertically and Crosswise The First by the First and the Last by the Last
Transpose and Apply For 7 the Multiplicand is 143
If the Samuccaya is the Same it is Zero By Osculation
If One is in Ratio the Other is Zero Lessen by the Deficiency
By Addition and by Subtraction Whatever the Deficiency lessen by that amount
and set up the Square of the Deficiency
By the Completion or Non-Completion Last Totalling 10
Differential Calculus Only the Last Terms
By the Deficiency The Sum of the Products
Specific and General By Alternate Elimination and Retention
The Remainders by the Last Digit By Mere Observation
The Ultimate and Twice the Penultimate The Product of the Sum is the Sum of the Products
By One Less than the One Before On the Flag**
The Product of the Sum  
All the Multipliers

 

Vedic Mathematics Sub-Sutras

 

S. No.

Sutras

Meaning

1.

Anurupyena

Proportionately

2.

Sisyate Sesasamjnah

Remainder remains constant

3.

Adyamadyenantyamantyena

First by first and last by last

4.

Kevalaih Saptakam Gunyat

In case of seven our multiplicand should be 143

5.

Vestanam

Osculation

6.

Yavdunam Tavdunam

Whatever the extent of its deficiency, lessen it still further to that very extent

7.

Yavdunam Tavdunam Varganchya Yojayet

Whatever the extent of its deficiency, lessen it still further to that very extent; and also set up the square of that deficiency.

8.

Antyayordasakepi

Whose last digits together total 10 and whose previous part is exactly the same

9.

Antyayoreva

Only the last terms

10.

Samuchchyagunitah

The sum of the coefficients in the product

11.

Lopanasthapanabhyam

By alternate elimination and retention

12.

Vilokanam

By observation

13.

Gunitsamuchchayah Samuchchayagunitah

The product of sum of the coefficients in the factors is equal to the sum of the coefficients in the product.

 

 

 

There are, of course, many questions which can be asked about this list: where does it come from? how can sixteen Sutras cover all of mathematics? why sixteen Sutras? what are sub-sutras and how are they related to the Sutras? if the Sutras are authentic how can they be validated? how are they structured? etc.

Sanskrit scholars have sought, so far without success, to find the Vedic text that contains the Sutras or the verses Bharati Krsna refers to. But even if they were found, this would not demonstrate that they govern or form a basis for mathematics, it would simply confirm that the system had a historical basis. So from a mathematical point of view this is not an important issue.

The word 'Sutra' means 'thread' and Bharati Krsna also uses the word 'aphorism'. An aphorism is 'a short pithy statement or maxim' (Concise Oxford Dictionary). If you have looked at the page, on this site, entitled Illustrative Examples and looked at the explanation given for the first example you will probably have noticed that the Sutra used does not give full details of how the calculation is done. This is because the Sutra gives an indication of the direction in which the mind has to go. In first looking at a question we may not know what to do- how do we begin to think about the problem? There are very many possibilities and the Sutra indicates a starting point; the rest of the method follows from that. The Sutras are very general and this is why they are so powerful and have such a wide range of application.

If the application of the Sutras is as universal as Bharati Krsna says they must refer to something more fundamental than what we usually think of as mathematics. With this in mind some research has related the Sutras to various functions of mind. We use our mind in certain definite and distinct ways: we may, for example, compare two ideas, or extend, reverse, generalise or vary an idea. These correlate neatly with the Sutras given and it is believed that they may give the key to explain the wide range of application of the Sutras. Much work still needs to be done on this but if it can be demonstrated that there are sixteen fundamental functions of mind and that these correspond to the sixteen given Sutras, a big step forward will have been taken, not just in establishing the authenticity of the Vedic system but also in explaining some fundamental issues in the philosophy of mathematics. Perhaps some cognitive psychologists will step forward and take up this challenge.

 

Some examples in Vedic Mathematics:

This section contains examples posted by me and others recently (June 1997) in IDD as is(Let me know if there are any critical typos). As I said, feel free to email me more stuff.

1. If you want to multiply any number with 9, 99, 999,...just use this rule: eg. 999x343=342657 (second number -1)(subtract 9 from each of these new digits)ie. 342 and (9-3)(9-4)(9-2)

2. If you want to square a number that is closer to 10, 100, 1000, ...: eg. 988^2=976144 (base number-(nearest '0' number - the base number))(square of the inner difference) ie. 988-(1000-988)and(1000-988)^2. I am at loss of words here, hope you get the idea.

3. If you want to square a number (that is not closer to 10, 1000,...): eg. 43^2=1849 (first digit x (the base number + second digit))(square of second digit) ie. (4 x (46))(3^2)=>1849

4. The square of any number ending in a five: (x5)^2 = [(x)(x+1)]25 Examples: 15^2 = ((1)(1+1))25 = 225 95^2 = (9(9+1))25 = 9025

5. The result of one over any number ending in a 9 can be computed in two very simple ways. I will give the easier example. 1/x9 ->

6. Here are examples, again for numbers closer to 10, 100, 1000... If you want to multiply two of these numbers, here are two cases: (Since folks are getting confused with syntax, I am just giving examples)

This logic above cannot be used for numbers that are not close to 10, 100,1000 etc

 

7..Ekadhikena Purvena Sutra (By one more than the one before) :

This method can be used for example to find squares of numbers ending in 5. For example, to find the square of 75, multiply the first number, 7, by "one more" which is 8. This is the first part of the answer. The last part is always 25. Voila! 5625 is the answer!


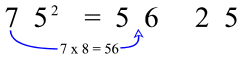
8.Urdhwa-tiryagbhyam (Vertically Crosswise):

This method can be employed to find the product of two numbers both close to 100 (or any other multiple of 10). For example, 88 is 12 below 100 and 98 is 2 below 100.

 The first part of the answer, 86, comes from subtracting crosswise: 88 - 2 = 86 (or 98 - 12 = 86: you can subtract
either way, you will always get the same answer)

The second part of the answer, 24, is just 12 x 2 : you multiply vertically.

So 88 x 98 = 8624. Could it get any easier?

Courtesy: To different Web pages